Pecout Hugues

Ingénieur d’études en sciences de l’information géographique

Cartographie, géomatique, analyse spatiale, documents computationnels, analyse de réseau, web scraping et fléchette

Caractèristiques : bruyant, gourmand et bien meilleur que Louis aux fléchettes
Programmation : quelques notions en langage R, exemple :

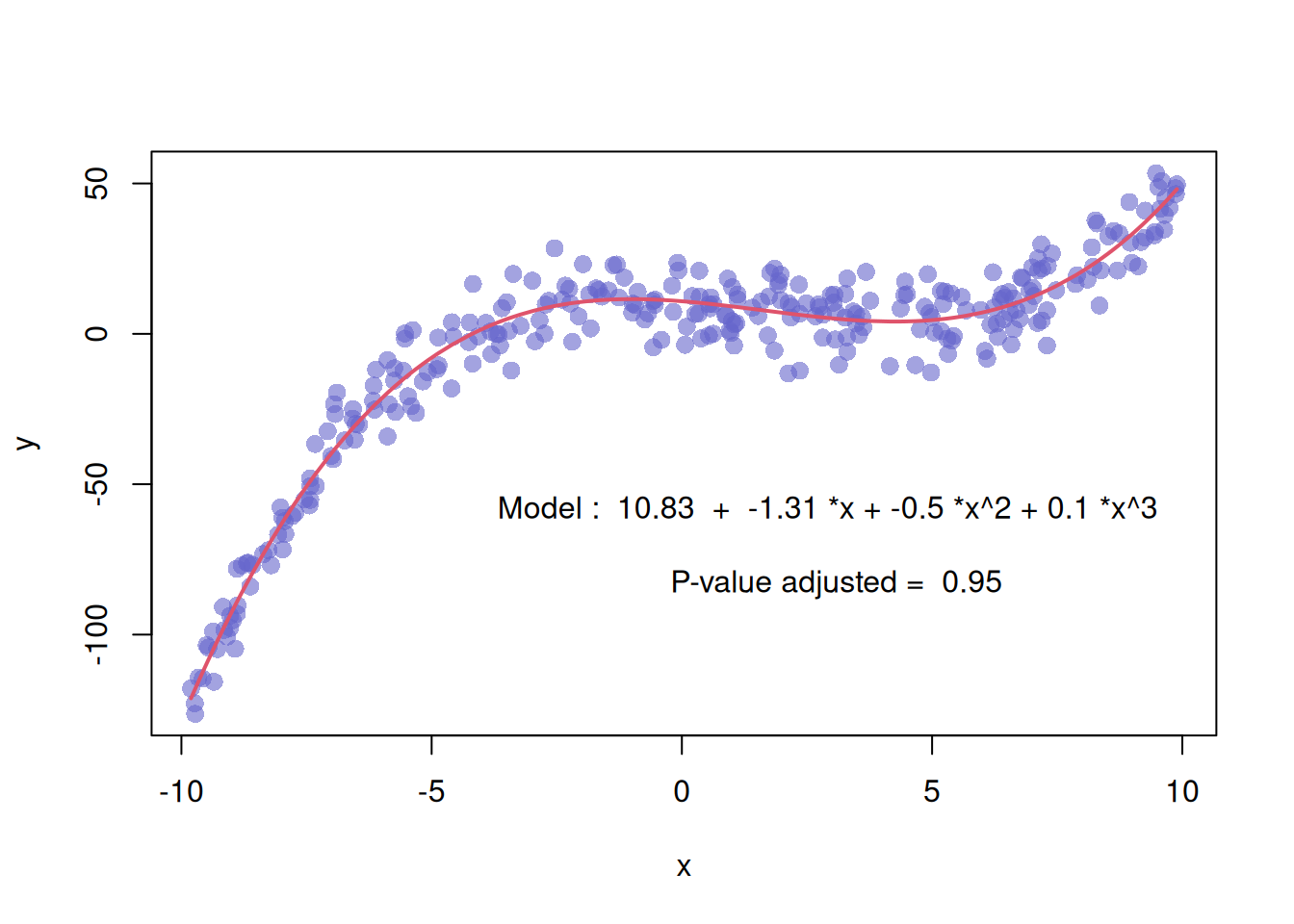
x <- runif(300,  min=-10, max=10) 
y <- 0.1*x^3 - 0.5 * x^2 - x + 10 + rnorm(length(x),0,8) 
 
# plot of x and y :
plot(x,y,col=rgb(0.4,0.4,0.8,0.6),pch=16 , cex=1.3) 
 
# Can we find a polynome that fit this function ?
model <- lm(y ~ x + I(x^2) + I(x^3))
 
# I can get the features of this model :
#summary(model)
#model$coefficients
#summary(model)$adj.r.squared
 
# For each value of x, I get the value of y estimated by the model
myPredict <- predict( model ) 
ix <- sort(x,index.return=T)$ix
lines(x[ix], myPredict[ix], col=2, lwd=2 )  

# I add the features of the model to the plot
coeff <- round(model$coefficients , 2)
text(3, -70 , paste("Model : ",coeff[1] , " + " ,
                    coeff[2] , "*x"  , "+" , 
                    coeff[3] , "*x^2" , "+" , 
                    coeff[4] , "*x^3" , "\n\n" , 
                    "P-value adjusted = ",
                    round(summary(model)$adj.r.squared,2)))

Tout cela n’est qu’illusion !

j’ai simplement copié-collé un bout de code R mis à disposition sur ce site

Ajout d’une modif